The Science of Tracking
To compute an orbit one has to determine both the position and velocity vectors of the spacecraft; these provide six of the seven necessary orbit parameters, the other being the time the measurement is made. [1] A tracking station measures the range and two angles to a spacecraft enabling the calculation of the first derivatives: range rate and two angle rates. Orbit predictions can then be produced from three sets of such data obtained in a single pass over a precision tracking station. Data from lower capability tracking stations can achieve the same results by triangulation from three of more stations.
The Requisites for Accurate Tracking
There are three basic requisites to achieve the required degree of tracking accuracy. The exact location of the tracking antenna must be established; the time at which each tracking measurement is made must be known precisely to a very high degree of accuracy; and the angular pointing of the antenna must be precisely calibrated.
A careful survey first establishes the positions of the antenna and its collimation tower. [2] A high precision tracking system also has an optical telescope built into its antenna, precisely aligned with the transmission axis. The collimation towers of such systems have a matching optical target and small antenna placed on the collimation tower in exactly the same relationship to each other as on the tracking antenna.
Meaningful tracking data requires every station in a network to have its epoch (local clock) set on Universal Time [3] and synchronized to within a few tens of millionths of a second of each other. This is usually accomplished by each station having an ‘atomic’ clock driven by a Caesium beam oscillator (or equivalent) stable to one part in ten thousand million (1 in 1010) - out by no more than 3 millionths of a second in 10,000 years. So important was the accuracy of the station’s ‘tick’ to accurate tracking that a travelling master atomic-clock visited each station clock after installation to establish the ‘tick’, and, at regular intervals thereafter, to check and synchronize it. Where range is measured by continuous-wave (CW) transmission, the necessary frequency stability is achieved by generating the transmitter frequency from the extremely stable oscillations of the same atomic standard that provides the ‘tick’.
Finally, the pointing accuracy of each system is confirmed optically by pointing the tracking antenna to a sequence of programmed positions in the night sky to determine if selected stars pass the cross hairs of the telescope at precisely the predicted times. This would not happen if any of the three common conditions had not been met.
#top
The Nature of Tracking
A tracking signal [4] is a propagated electromagnetic (radio) wave that travels at the speed of light; 299,792,458 m/sec. Several parameters - frequency, wavelength, velocity, amplitude, and directivity - can be determined for such a wave. [5] Measurement of these reveal several ‘particulars’ that are modified as a consequence of the path travelled by the wave: propagation time, phase delay, frequency shift and amplitude.
The amplitude of a signal, apart from telling us whether an antenna is pointed directly at the source of the signal, has no practical use in measuring range. The other three particulars are closely related, e.g. “a measurement of propagation time is actually a direct time measurement of the phase delay of the signal.” [6]
A different technique of measurement has developed around each of the three remaining particulars: phase-delay, phase-rate, and relative-phase. All six tracking systems at CRO utilized two or more of them.
#top
Range: Phase-delay measurement
Measurements of phase delay (or propagation time) [7] are directly related to the total length of the transmission path, to the spacecraft and back again. When the ground transmitter and receiver are at the same place, the one-way trip time is exactly half of the total trip time. The range can then be easily calculated by multiplying the speed of light (c) by half the total-trip time (t), i.e. ct/2.
Either pulsed or CW signals can be used to determine range. With the pulsed signals of radar systems the total-trip time is measured directly: it is the time interval between the transmission of a pulse from the radar and the reception of that same pulse returned by the spacecraft either by skin reflection or transponder. [8]
The process of determining phase delay is somewhat more complex with CW signals than it is with pulse signals. CW ranging depends on maintaining a coherent [9] relationship from the initial transmitted signals to a spacecraft transponder (which maintains the coherence) and back again to a phase comparison between the transmitted and received signals at the ground station.
Pulse radars
Carnarvon had two pulse radars, the FPQ-6 and the VERLORT (VERy LOng Range Tracking) radar. The FPQ-6 radar had a built-in computer and was accurate enough to be able to develop a complete orbit prediction by calculating the necessary first derivatives from the angle and distance data it measured.
#top
Continuous-wave RARR
A GRARR station consisted of a VHF system for near-Earth scientific missions and an S-band system for cis-lunar [10] space.
The VHF system used six tones from 20 kHz to 8Hz in 5:1 frequency increments. The tones below 4 kHz were modulated onto a 4 kHz sub-carrier to provide sufficient separation between the carrier and the side bands. Two tones at a time were transmitted; the lower tone produced the ranging information and the higher tone ensured a finer measurement resolution. A replica of the transmitted tone was phase shifted in the ground receiver until it matched the received low tone: the amount of shift was a direct measurement of the total-trip time. The lowest tone (8Hz) provided a non-ambiguous maximum range of 18,737km, just one twentieth of the distance to the Moon. Orbits with higher ranges can still be supported because of prior knowledge of the approximate range.
The S-band system used two higher tones, 500 kHz and 100 kHz, for even more precise resolution of range but otherwise operated just the same as the VHF system. Modelled after the USB code ranging system, an Ambiguity-Resolving Code (ARC) sub-system was retrofitted to GRARR to extend its non-ambiguous range capability to 1,213,597km, almost four times the distance to the Moon. It consisted of two pseudo-random [11] sub-codes of 255 and 127 bits combined to produce a combined code of 32385 bits. After an ambiguous tone result had been determined, the tones were removed and the ranging code was then modulated onto the 4 kHz sub-carrier at 4000bps. The ground receiver phase shifted a replica of the ranging code in 500 bit steps by moving the two sub-codes by 10 bits and 5 bits respectively, until a bit-for-bit correlation was achieved with the received code; this gave a direct measurement of the total-trip time. Block stepping of sub-codes achieved a much faster result than by stepping the combined code one bit at a time.
#top
Continuous-wave USB
The MSFN USB PRN [12] ranging system only ever used digital codes. These consisted of five pseudo-random codes, mostly of prime number length, combined to generate a 5,456,682-bit pseudo-random code transmitted at 100kbs and giving a maximum unambiguous range of 804,650km, nearly three times the distance to the Moon. The USB range resolution was ±1m, however system jitter and ground instabilities downgraded this to about ±15m. The code-stepping correlation technique for the USB ranging codes was essentially the same as for GRARR ARC sub-system.
#top
Range Rate: Phase-rate measurement
Any movement of the spacecraft towards or away from the ground station will cause the returned carrier signal to show an apparent frequency shift, known as Doppler. The Doppler shift is directly proportional to the rate of change of path length from the transmitter to the spacecraft, i.e. range rate – the direct measurement of the first derivative of range. When the ground transmitter and receiver are at the same location the extracted frequency shift is ± 2Dα where Dα is the Doppler shift on the uplink signal.
On both the USB and GRARR systems, digital and tone codes were removed once ranging had been achieved. The range of the spacecraft could then be maintained by integrating the range rate (Doppler) measurement with the already-measured range value.
It is important to note that Doppler shift only gives the range rate along the line extended from the transmitter through the spacecraft: when there is no relative movement there is a zero Doppler shift. To get a complete three-dimensional picture, an RARR spacecraft usually has three independent VHF transponders to enable three widely spaced tracking stations to simultaneously perform a triangulation on the spacecraft’s position and movement. A single S-band transponder is usual for more distant ranging where triangulation is less important.
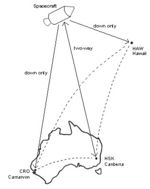
Similarly triangulation was performed on the Apollo spacecraft by three MSFN USB tracking stations such as Carnarvon (CRO), Honeysuckle Creek (HSK) and Hawaii (HAW). In this case only the prime station, HSK, got true Doppler from the Apollo’s single transponder while the other two stations extracted pseudo-Doppler based on their extremely high accuracy receiver reference frequencies. Even so, this solution was ten times more accurate than a single station track. [13]
Spacecraft position can be calculated entirely without angle data from three tracking stations using a triangulation technique - just simple spherical trigonometry with the known base-line lengths between the stations and the measured ranges intersecting at the spacecraft ‘apex’.
#top
Angle: Relative–phase measurement
The third technique relies on relative or interferometer-type, rather than absolute, phase measurement. This technique can be the basis of tracking from a number of long base-line stations. But at CRO it was used as a monopulse technique where every tracking antenna independantly compared four different off-axis beams simultaneously.
Consider a tracking antenna that is pointing directly at a spacecraft. Each part of the Antenna’s surface will be equally distant from the spacecraft so there will be no apparent phase difference. If the antenna is pointing slightly away from the spacecraft, one edge of the antenna will now be closer and the opposite edge will be further away – a difference in signal path length. This will produce a ‘relative’ phase difference between the signals received by the two sides of the antenna: this difference can be used to generate an error signal that will drive the antenna to restore the phase balance.
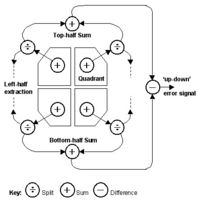
Tracking antennas have two drive systems which act perpendicular to each other so that an antenna can be pointed to any point in the sky using the right combination of instructions to its two drive motors. The Acquisition Aid (Acq Aid) was a typical example. Its array of eighteen small turnstile antennas was evenly spread over a wire-screen ground plane. The signal outputs from each quadrant of the screen were summed so that they could be compared in specific ways to create the two sets of error signals. Each quadrant sum was split in two and each split was summed again in four pairs to form top-half, bottom-half, left-half, and right-half outputs. The phase difference between the ‘top’ and the ’bottom’ outputs, generates an ‘up-down’ error signal and that between the ‘left’ and ‘right’ outputs generates a ‘sideways’ error signal. The angle measurement technique on the GRARR VHF was essentially the same.
The Q6, VERLORT, USB and GRARR S-band antennas were all parabolic dish reflectors focussing the received signal via a sub-reflector onto a four-aperture horn in the centre of the dish [14]. Signals from the four apertures generated error signals in a similar manner to the four quadrants of the Acq Aid and the GRARR VHF antennas.
#top
References
[1] ‘spaceguard.esa.int/Nscience/neo/neo-where/orbit-char.htm’ is a useful primer on orbital parameters.
[2] The collimation tower (or bore-sight) is used for calibration and for checking system performance.
[3] Sometimes known as Greenwich Mean Time (GMT) or Zulu Time.
[4] The organisation of the remainder of this Technical Note is based on Gruenberg, E.L. 3-42 to -46.
[5] Gruenberg, E.L., 3-43.
[6] Gruenberg, E.L., op cit.
[7] Details of the GRARR and USB systems are based on Kronmiller, G.G. and Baghdady, E.J. (from notes provided by B. Heald); on NASA publication ‘Equipment Manning and Information for the Carnarvon Facility’; and on my personal knowledge of the two systems (PD).
[8] The metallic skin of the spacecraft reflects a radio wave as it would a light wave. The transponder receives the signal and retransmits it at a higher frequency in the ratio of 240:221, the ‘International Friend or Foe’ (IFF) standard.
[9] In this context, ‘coherent’ means there is a fixed relationship between the frequency and phase of the input and output signals at the spacecraft transponder, i.e. the output signal acts in unison with the input signal.
[10] ‘Cis-lunar space’ is that region between the Earth and the Moon where the gravitational influence of both bodies on the spacecraft is profound.
[11] A truly random code would have an equal number of ‘1’s and ‘0’s with no predictable pattern - even to infinity. A pseudo-random code is designed to have the same balance of ‘1’s and ‘0’s: this ensures that there is no DC bias in the modulated carrier, and for the duration of the combined code repeat, there is no discernable internal pattern hence no chance of a false correlation.
[12] Pseudo-random codes are combined to form a range signal emulating a pseudo-random noise (PRN) signal which has an equal number of ‘1’ and ‘0’ bits; this avoids an overall DC bias in the carrier signal.
[13] Vonbun, F.O., p.19.
[14] The Q6 radar had a five-horn feed system to reduce the possibility of a side-lobe lock-on.